3. Reconstruction of the coastal wave climate with RBF¶
Cases are already propagated and we now have a lot of different waves with different characteristics propagated all along the coast so the reconstruction of the wave climate can be done.
The reconstruction of the wave climate in shallow waters is carried out by an interpolation from the selected case series that have been propagated from undefined depths. The interpolation technique used is based on radial basis functions (RBF), very suitable for data with high dimensionality and not evenly distributed. There is a series of values of the real function \(f(x_i) \:\:\: i = 1, ..., N\) in the points \(x_1 , ..., x_N\). The RBF interpolation technique considers that the RBF function approximation consists of a linear combination of symmetrical radial functions centered on the given points. The objective function has the following expression:
interpolating the given values as follows:
where \(RBF\) is the interpolation function, \(p(x)\) is the linear polynomial in all the variables involved in the problem, \(a_i\) are the RBF adjustment coefficients, \(\Phi\) is the basic radial function, \(||\cdot||\) is the Euclidean norm and \(x_i\) are the centres of the RBF interpolation.
The polynomial \(p(x)\) in the expression of the RBF interpolation function is defined as a monomial base \({p_0, p_1 ,..., p_d}\). The first is a monomial, consisting of a number of grade one monomials equal to the dimensionality of the data, where \(b = {b_0 , b_1 ,..., b_d}\) are the coefficients of these monomials.
The radially based functions can have different expressions. Some of these radial functions contain a shape parameter that plays a very important role in the precision of the technique. In the methodology of propagation of the maritime climate, it has been considered the Gaussian radial function that depend on a shape parameter.
Notice that the RBF reconstruction is done for each CSIRO reanalysis partition, but all these partitions must be grouped together for the buoy validation and the final estimations of both the profile of the beach and the surfing regional index, which will be added to the repository in the future.
In this last paragraph, new concepts have been introduced. First, CSIRO is the name that the wave reanalysis receives and last, these two new concepts of profile analysis and surfing regional index will be added, but a detailed explanation can be seen in the attached pdf, (Javier Tausia, 2020).
# common
import sys
import os
import os.path as op
# basic
import xarray as xr
import numpy as np
import pandas as pd
from datetime import timedelta as td
from matplotlib import pyplot as plt
from pandas.plotting import register_matplotlib_converters
# warnings
import warnings
warnings.filterwarnings("ignore")
# dev library
sys.path.insert(0, os.getcwd())
# RBF module
from rbf_main import RBF_Reconstruction
import rbf_functions as rbff
Once the modules are imported, the preprocessing must be done, as usually. For this purpose, please just edit the selected parts, as if data is changed, it could not work. If the propagations have not been performed using the proportioned SWAN notebook, the shape of this data must match the used shape.
p_data = op.join(os.getcwd(), '..', 'data')
p_swan = op.join(p_data, 'projects-swan')
# -------------- EDIT THIS PART --------------------------------------------- #
name = 'SDR' # used name in the SWAN section
name_file = 'virgen-buoy' # name for the file
resolution = str(0.0024) # used resolution in the SWAN section (see the folder name)
num_cases = str(300) # num cases in the SWAN section
# --------------------------------------------------------------------------- #
# SUBSETS
subsetsea = pd.read_pickle(op.join(p_swan, name+'-SEA-'+resolution,
'sea_cases_'+num_cases+'.pkl'))
subsetsea = subsetsea[['hs', 'per', 'dir', 'spr']]
subsetswell = pd.read_pickle(op.join(p_swan, name+'-SWELL-'+resolution,
'swell_cases_'+num_cases+'.pkl'))
subsetswell = subsetswell[['hs', 'per', 'dir', 'spr']]
# TARGETS
targetsea = xr.open_dataset(op.join(p_swan, name+'-SEA-'+resolution,
'sea_propagated_'+num_cases+'.nc'))
targetswell = xr.open_dataset(op.join(p_swan, name+'-SWELL-'+resolution,
'swell_propagated_'+num_cases+'.nc'))
# Reconstruction desired point
# ------- EDIT THE DESIRED POINT ------- #
# - Coordinates as shown in GoogleMaps - #
lat = 43.49
lon = -3.88
# -------------------------------------- #
# if an error occurs, please have a look at the
# resolution of the bathymetry/propagations and
# edit the reconstruction point
lat = np.where((targetsea.Y.values<lat+0.0012) &
(targetsea.Y.values>lat-0.0012))[0][0]
lon = np.where((targetswell.X.values<lon+0.0012) &
(targetswell.X.values>lon-0.0012))[0][0]
targetsea = targetsea.isel(X=lon).isel(Y=lat)
targetswell = targetswell.isel(X=lon).isel(Y=lat)
targetsea = pd.DataFrame({'hs': targetsea.Hsig.values,
'per': targetsea.TPsmoo.values,
'perM': targetsea.Tm02.values,
'dir': targetsea.Dir.values,
'spr': targetsea.Dspr.values})
seaedit = subsetsea.mean()
seaedit['perM'] = 7.0
targetsea = targetsea.fillna(seaedit)
targetswell = pd.DataFrame({'hs': targetswell.Hsig.values,
'per': targetswell.TPsmoo.values,
'perM': targetswell.Tm02.values,
'dir': targetswell.Dir.values,
'spr': targetswell.Dspr.values})
swelledit = subsetswell.mean()
swelledit['perM'] = 12.0
targetswell = targetswell.fillna(swelledit)
# DATASETS
dataset_tot = pd.read_pickle(op.join(p_data, 'hindcast',
'csiro_dataframe_sat_corr.pkl'))
print(dataset_tot.info())
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 360840 entries, 1979-01-01 00:00:00 to 2020-02-29 23:00:00
Data columns (total 29 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Hs 360840 non-null float32
1 Tm_01 360839 non-null float32
2 Tm_02 360840 non-null float32
3 Tp 360839 non-null float32
4 DirM 360839 non-null float32
5 DirP 360839 non-null float32
6 Spr 360839 non-null float32
7 Nwp 360840 non-null float32
8 U10 360840 non-null float32
9 V10 360840 non-null float32
10 W 360840 non-null float64
11 DirW 360832 non-null float64
12 Hsea 360840 non-null float32
13 Hswell1 360840 non-null float32
14 Hswell2 360840 non-null float32
15 Hswell3 360840 non-null float32
16 Tpsea 172510 non-null float32
17 Tpswell1 321377 non-null float32
18 Tpswell2 138960 non-null float32
19 Tpswell3 46833 non-null float32
20 Dirsea 172510 non-null float32
21 Dirswell1 321377 non-null float32
22 Dirswell2 138960 non-null float32
23 Dirswell3 46833 non-null float32
24 Sprsea 172510 non-null float32
25 Sprswell1 321377 non-null float32
26 Sprswell2 138960 non-null float32
27 Sprswell3 46833 non-null float32
28 Hs_cal 360840 non-null float32
dtypes: float32(27), float64(2)
memory usage: 45.4 MB
None
# Choose the seas and swells to perform the reconstruction as shown:
# as mentioned in previous notebooks, please edit if more partitions exist
labels_input = [['Hsea', 'Tpsea', 'Dirsea', 'Sprsea'],
['Hswell1', 'Tpswell1','Dirswell1', 'Sprswell1'],
['Hswell2', 'Tpswell2','Dirswell2', 'Sprswell2'],
['Hswell3', 'Tpswell3','Dirswell3', 'Sprswell3']]
labels_output = [['Hsea', 'Tpsea', 'Tm_02', 'Dirsea', 'Sprsea'],
['Hswell1', 'Tpswell1', 'Tm_02','Dirswell1', 'Sprswell1'],
['Hswell2', 'Tpswell2', 'Tm_02','Dirswell2', 'Sprswell2'],
['Hswell3', 'Tpswell3', 'Tm_02','Dirswell3', 'Sprswell3']]
datasets = []
for ss in labels_input:
dataset_ss = dataset_tot[ss]
dataset_ss = dataset_ss.dropna(axis=0, how='any')
datasets.append(dataset_ss)
dataframes = []
print('Performing RFB reconstruction... \n')
# RBF
for count, dat in enumerate(datasets):
# Scalar and directional columns
ix_scalar_subset = [0,1,3]
ix_directional_subset = [2]
ix_scalar_target = [0,1,2,4]
ix_directional_target = [3]
# RBF for the seas
if count==0:
# Calculating subset, target and dataset
subset = subsetsea.to_numpy()
target = targetsea.to_numpy()
dat_index = dat.index
dataset = dat.to_numpy()
# Performing RBF
output = RBF_Reconstruction(
subset, ix_scalar_subset, ix_directional_subset,
target, ix_scalar_target, ix_directional_target,
dataset
)
# Reconstrucing the new dataframe
for l, lab in enumerate(labels_output[count]):
if l==0:
output_dataframe = pd.DataFrame({lab: output[:,l]},
index=dat_index)
else:
output_dataframe[lab] = output[:,l]
# Appending all new dataframes
dataframes.append(output_dataframe)
# RBF for the swellls
else:
# Calculating subset, target and dataset
subset = subsetswell.to_numpy()
target = targetswell.to_numpy()
dat_index = dat.index
dataset = dat.to_numpy()
# Performing RBF
output = RBF_Reconstruction(
subset, ix_scalar_subset, ix_directional_subset,
target, ix_scalar_target, ix_directional_target,
dataset
)
# Reconstrucing the new dataframe
for l, lab in enumerate(labels_output[count]):
if l==0:
output_dataframe = pd.DataFrame({lab: output[:,l]},
index=dat_index)
else:
output_dataframe[lab] = output[:,l]
# Appending all new dataframes
dataframes.append(output_dataframe)
# Join final file
reconstructed_dataframe = pd.concat(dataframes, axis=1)
# But we first maintain just one Tm, as they are all the same
Tm_02 = reconstructed_dataframe['Tm_02'].mean(axis=1)
reconstructed_dataframe = reconstructed_dataframe.drop(columns=['Tm_02'])
reconstructed_dataframe['Tm_02'] = Tm_02
Performing RFB reconstruction...
ix_scalar: 0, optimization: 7.11 | interpolation: 9.79
ix_scalar: 1, optimization: 14.49 | interpolation: 10.68
ix_scalar: 2, optimization: 5.83 | interpolation: 13.65
ix_scalar: 4, optimization: 6.96 | interpolation: 16.33
ix_directional: 3, optimization: 18.71 | interpolation: 23.13
ix_scalar: 0, optimization: 7.27 | interpolation: 19.68
ix_scalar: 1, optimization: 13.05 | interpolation: 23.09
ix_scalar: 2, optimization: 14.35 | interpolation: 24.45
ix_scalar: 4, optimization: 7.09 | interpolation: 21.10
ix_directional: 3, optimization: 12.56 | interpolation: 35.68
ix_scalar: 0, optimization: 5.95 | interpolation: 7.50
ix_scalar: 1, optimization: 12.35 | interpolation: 7.96
ix_scalar: 2, optimization: 16.53 | interpolation: 8.52
ix_scalar: 4, optimization: 5.47 | interpolation: 7.69
ix_directional: 3, optimization: 11.92 | interpolation: 14.93
ix_scalar: 0, optimization: 5.62 | interpolation: 2.54
ix_scalar: 1, optimization: 12.96 | interpolation: 2.62
ix_scalar: 2, optimization: 12.71 | interpolation: 2.65
ix_scalar: 4, optimization: 5.06 | interpolation: 2.62
ix_directional: 3, optimization: 14.09 | interpolation: 5.05
# Saving
# reconstructed_dataframe.to_pickle(op.join(p_data, 'reconstructed',
# 'reconstructed_partitioned_'+name_file+'.pkl'))
# print(reconstructed_dataframe)
Once the reconstruction has been performed, we now have different partitions propagated in the selected point. These propagations can be added to obtain the requested bulk variables for both the validation with coastal buoys and the creation of the surfing index if wanted. This can be done using two different methods:
Bulk parameters
Spectral parameters
In this case, we will use the bulk reconstruction, as it is easier and much more important, faster, but a notebook is also added that uses the spectral reconstruction, explained in detail there.
For the bulk or aggregated conditions, the following formulas are used to calculate the significant wave height, the wave peak period and the wave mean direction:
where using them, these aggregated parameters can be obtained, leading to a complete reconstructed dataframe in the desired point.
# First copy to play with NaNs
agg = reconstructed_dataframe.copy()
agg[['Tpsea', 'Tpswell1', 'Tpswell2', 'Tpswell3']] = \
agg[['Tpsea', 'Tpswell1', 'Tpswell2', 'Tpswell3']].fillna(np.inf)
agg = agg.fillna(0.0)
# Bulk Hs
reconstructed_dataframe['Hs_Agg'] = np.sqrt(
agg['Hsea']**2 +
agg['Hswell1']**2 +
agg['Hswell2']**2 +
agg['Hswell3']**2
)
# Bulk Tp
reconstructed_dataframe['Tp_Agg'] = np.sqrt(
reconstructed_dataframe['Hs_Agg']**2 / (agg['Hsea']**2/agg['Tpsea']**2 +
agg['Hswell1']**2/agg['Tpswell1']**2 +
agg['Hswell2']**2/agg['Tpswell2']**2 +
agg['Hswell3']**2/agg['Tpswell3']**2)
)
# Second copy to play with NaNs
agg = reconstructed_dataframe.copy().fillna(0.0)
# Bulk Dir
reconstructed_dataframe['Dir_Agg'] = np.arctan(
(agg['Hsea']*agg['Tpsea']*np.sin(agg['Dirsea']*np.pi/180) +
agg['Hswell1']*agg['Tpswell1']*np.sin(agg['Dirswell1']*np.pi/180) +
agg['Hswell2']*agg['Tpswell2']*np.sin(agg['Dirswell2']*np.pi/180) +
agg['Hswell3']*agg['Tpswell3']*np.sin(agg['Dirswell3']*np.pi/180)) /
(agg['Hsea']*agg['Tpsea']*np.cos(agg['Dirsea']*np.pi/180) +
agg['Hswell1']*agg['Tpswell1']*np.cos(agg['Dirswell1']*np.pi/180) +
agg['Hswell2']*agg['Tpswell2']*np.cos(agg['Dirswell2']*np.pi/180) +
agg['Hswell3']*agg['Tpswell3']*np.cos(agg['Dirswell3']*np.pi/180))
)
reconstructed_dataframe['Dir_Agg'] = reconstructed_dataframe['Dir_Agg']*180/np.pi
reconstructed_dataframe['Dir_Agg'] = reconstructed_dataframe['Dir_Agg'].where(reconstructed_dataframe['Dir_Agg']>0,
reconstructed_dataframe['Dir_Agg']+360)
# Wind features
reconstructed_dataframe = reconstructed_dataframe.join(dataset_tot[['W', 'DirW']])
# In case coastal buoy exists
print('Extracting Buoy information...')
buoy = pd.read_pickle(op.join(p_data, 'buoy', 'dataframe_vir.pkl')) # this data is an example
# the buoy is located in the north of Spain
buoy.index = buoy.index.round('H')
buoy = buoy.drop_duplicates()
buoy_index = sorted(buoy.index.values)
Extracting Buoy information...
print(reconstructed_dataframe.info())
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 360839 entries, 1979-01-01 01:00:00 to 2020-02-29 23:00:00
Freq: H
Data columns (total 22 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Hsea 172510 non-null float64
1 Tpsea 172510 non-null float64
2 Dirsea 172510 non-null float64
3 Sprsea 172510 non-null float64
4 Hswell1 321377 non-null float64
5 Tpswell1 321377 non-null float64
6 Dirswell1 321377 non-null float64
7 Sprswell1 321377 non-null float64
8 Hswell2 138960 non-null float64
9 Tpswell2 138960 non-null float64
10 Dirswell2 138960 non-null float64
11 Sprswell2 138960 non-null float64
12 Hswell3 46833 non-null float64
13 Tpswell3 46833 non-null float64
14 Dirswell3 46833 non-null float64
15 Sprswell3 46833 non-null float64
16 Tm_02 360839 non-null float64
17 Hs_Agg 360839 non-null float64
18 Tp_Agg 360839 non-null float64
19 Dir_Agg 360839 non-null float64
20 W 360839 non-null float64
21 DirW 360831 non-null float64
dtypes: float64(22)
memory usage: 73.3 MB
None
reconstructed_dataframe.to_pickle(op.join(p_data, 'reconstructed',
'reconstructed_'+name_file+'.pkl'))
3.1. Results comparison - (Hindcast | Buoy)¶
total = reconstructed_dataframe.join(buoy, how='inner')
total_plot = total[['Hs_Buoy', 'Tp_Buoy', 'Dir_Buoy',
'Hs_Agg', 'Tp_Agg', 'Dir_Agg',
# 'Hs_Spec', 'Tp_Spec', 'Dir_Spec',
'Hsea', 'Tpsea', 'Dirsea',
'Hswell1', 'Tpswell1', 'Dirswell1']]
labels = ['$H_S$ [m]', '$T_P$ [s]', '$\u03B8$ [$\degree$]']
validation_data = total_plot.copy()
register_matplotlib_converters()
year = 2009
name_buoy = 'Virgen del Mar'
ini = str(year)+'-01-01 00:00:00'
end = str(year)+'-12-31 23:00:00'
total_plot = total_plot.loc[ini:end]
fig, axs = plt.subplots(3, 1, figsize=(20,15), sharex=True)
fig.subplots_adjust(hspace=0.05, wspace=0.1)
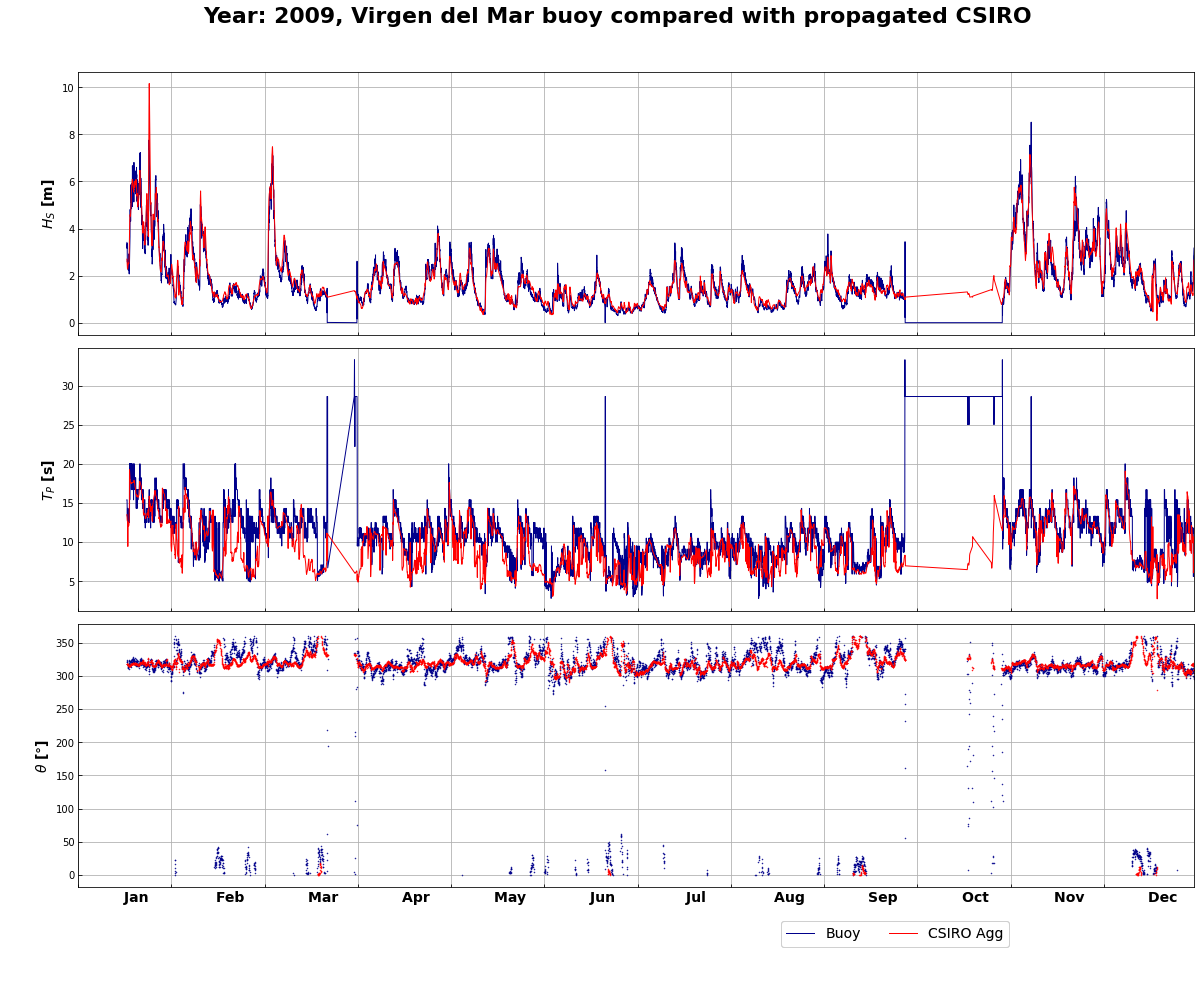
fig.suptitle('Year: ' +str(year)+ ', ' +name_buoy+ ' buoy compared with propagated CSIRO',
fontsize=22, y=0.94, fontweight='bold')
months = [' Jan', ' Feb', ' Mar',
' Apr', ' May', ' Jun',
' Jul', ' Aug', ' Sep',
' Oct', ' Nov', ' Dec']
i = 0
while i < 3:
if i==2:
axs[i].plot(total_plot[total_plot.columns.values[i]], '.', markersize=1, color='darkblue')
axs[i].plot(total_plot[total_plot.columns.values[i+3]], '.', markersize=1, color='red')
#axs[i].plot(total_plot[total_plot.columns.values[i+6]], '.', markersize=1, color='darkgreen')
#axs[i].plot(total_plot[total_plot.columns.values[i+9]], '.', markersize=1, color='orange')
#axs[i].plot(total_plot[total_plot.columns.values[i+12]], '.', markersize=1, color='purple')
axs[i].set_ylabel(labels[i], fontsize=14, fontweight='bold')
axs[i].grid()
axs[i].set_xlim(ini, end)
axs[i].set_xticks(np.arange(pd.to_datetime(ini), pd.to_datetime(end), td(days=30.5)))
axs[i].tick_params(direction='in')
axs[i].set_xticklabels(months, fontsize=14, fontweight='bold')
else:
axs[i].plot(total_plot[total_plot.columns.values[i]], color='darkblue', linewidth=1)
axs[i].plot(total_plot[total_plot.columns.values[i+3]], color='red', linewidth=1)
#axs[i].plot(total_plot[total_plot.columns.values[i+6]], color='darkgreen', linewidth=1)
#axs[i].plot(total_plot[total_plot.columns.values[i+9]], color='orange', linewidth=1)
#axs[i].plot(total_plot[total_plot.columns.values[i+12]], color='purple', linewidth=1)
axs[i].set_ylabel(labels[i], fontsize=14, fontweight='bold')
axs[i].grid()
axs[i].tick_params(direction='in')
fig.legend(['Buoy', 'CSIRO Agg',
#'CSIRO Spec'
], loc=(0.65, 0.04), ncol=3, fontsize=14)
i += 1
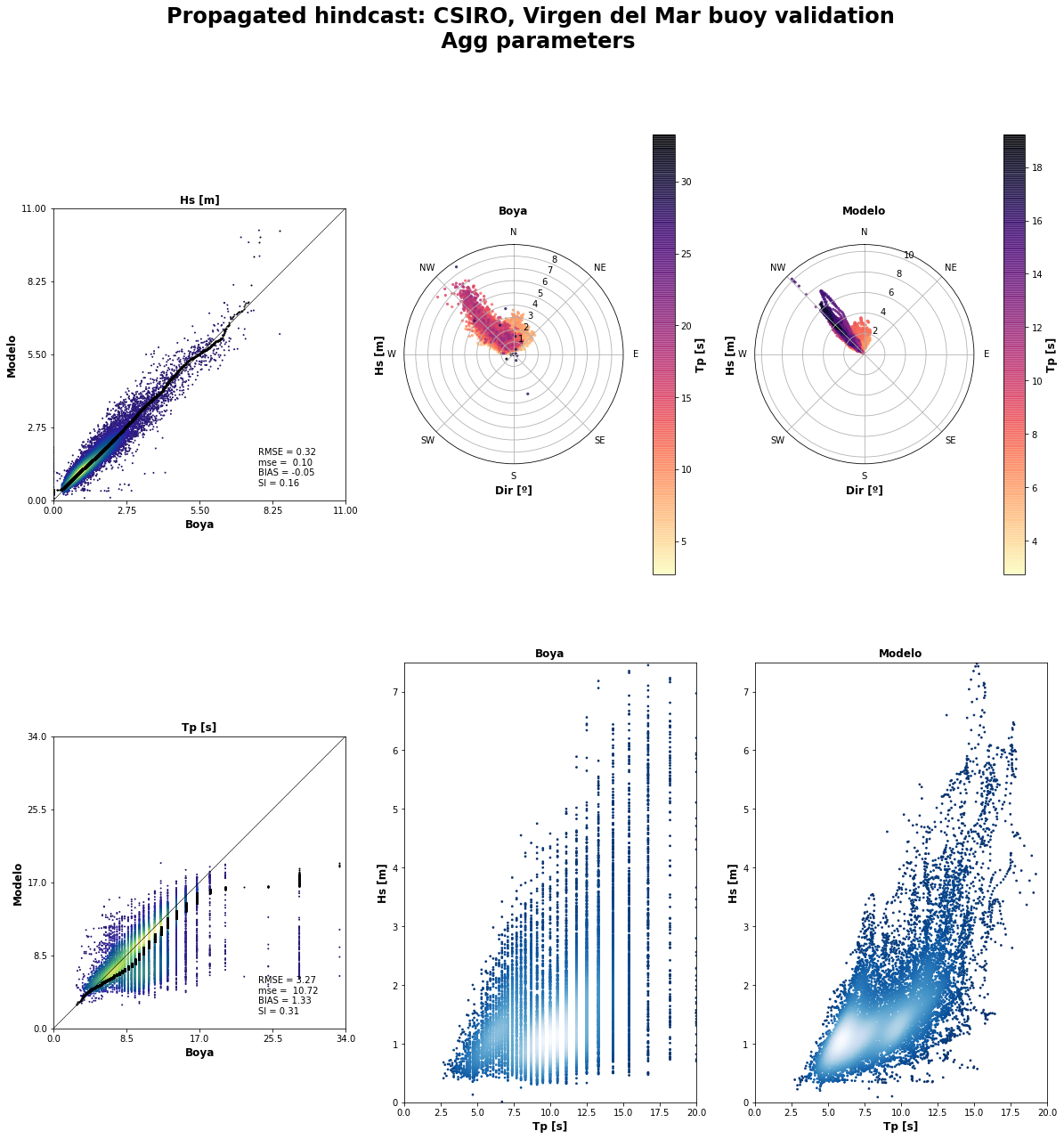
rbff.buoy_validation(validation_data, name_buoy, 'agg')
# rbff.buoy_validation(validation_data, name_buoy, 'spec')
--------------------------------------------------------
AGG VALIDATION will be performed
--------------------------------------------------------
Validating and plotting validated data...
Length of data to validate: 13843